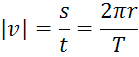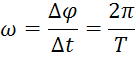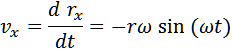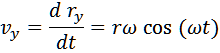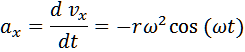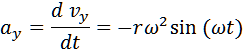MOTO CIRCOLARE UNIFORME

ATTIVITA'

Il cerchietto bianco mette in evidenza il moto del solco sotto la testina del braccio del giradischi.

 

Verificare se il tempo necessario a compiere un giro per un solco più esterno e quello per il solco più interno sono uguali.

 

Premendo il pulante START si avvia il giradischi (un vecchio 33 giri)
Prendo il pulsante MISURA si legge il tempo  dell'orologio e la distanza della testina magnetica dal centro del piatto (raggio). I due valori vengono registrati nelle rispettive colonne.
Il tempo impiegato a fare un giro (periodo) è dato dalla differenza di due tempi successivi. Per avere un punto di riferimento possiamo misurare il tempo quando il cerchietto bianco passa sotto la testina magnetica.

Possiamo sospendere la simulazione premendo STOP e riavviarla premendo START. Per riposizionare la testina (pickup) all'inizio premere RESTART.
Possiamo ripetere le misure con un raggio diverso agendo sul cursore "raggio", rispettando la sequenza: STOP > RESTART > definire raggio > START.
 

Conoscendo il periodo medio e il raggio medio calcolare la velocità del cerchietto bianco (velocità tangenziale).
Come varia il periodo al variare del raggio?
Come varia la velocità tangenziale al variare del raggio?
Puoi scrivere una relazione tra raggio e velocità tangenziale?
 

NOTA

La velocità della simulazione è rallentata, ma ciò non influisce sui tempi registrati.

Abbiamo ripetuto le misure per 5 valori del raggio.	Elaborazione misure
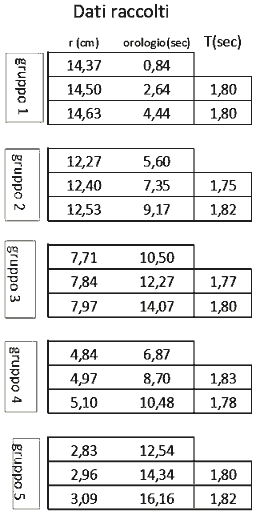	T è il periodo, cioè il tempo impiegato a fare un giro completo: si calcola come differenza fra due letture successive dell'orologio. La velocità tangenziale è la velocità con cui si muove il cerchietto sul solco del disco. La velocità angolare è l'angolo spazzolato nell'unità di tempo
le misure sono state prese quando il cerchietto passava sotto la testina del giradischi. Tenendo conto dei tempi di reazione della mano possiamo stimare un errore nella lettura dei tempi pari a 0,1 sec.	La frequenza è il numero di giri nell'unità di tempo. Nota: il periodo, entro gli errori sperimentale, è costante (circa 1,8 sec). La velocità tangenziale aumenta con il raggio. Vedi teoria

Un corpo si muove di MOTO CIRCOLARE UNIFORME se si sposta su una traiettoria circolare con una  velocità di modulo costante.

 

	Il vettore velocità istantanea v è sempre tangente alla traiettoria (in questo caso il cerchio) e quindi è perpendicolare a r, vettore posizione Si poteva arrivare alla stessa conclusione osservando che essendo la traiettoria un cerchio, il modulo di r rimane costante e quindi v non può avere una componente lungo r, cioè è perpendicolare a r
	In un tempo Δt il corpo si è spostato dalla posizione A, individuata dal vettore r, alla posizione A’, individuata da r’, percorrendo un arco di cerchio Δs. Nello steso tempo r ha spazzolato un angolo φ. Δs= v Δt   Δs = rφ= v Δt da cui è la velocità angolare cioè l’angolo spazzolato nell’unità di tempo ed è generalmente indicata con ω
	velocità angolare
	velocità tangenziale
	spostamento sulla circonferenza
Il periodo T è il tempo impiegato dall’oggetto a compiere un giro completo
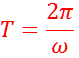	Periodo
La frequenza  f è il numero di giri effettuati in 1 secondo:    f=1/T
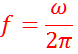	Frequenza

L'accelerazione nasce dal fatto che il vettore velocità, pur mantenendo il modulo costante, cambia continuamente direzione.

Per calcolare a sfruttiamo l'uguaglianza formale fra le relazioni tra v e r e le relazioni tra a e v e quindi applichiamo formalmente all'accelerazione le stesse formule che abbiamo trovato per la velocità tangenziale

 

 

Analizziamo meglio la similitudine:

trasliamo i vettori velocità in C: v →u ; v'→ u'

l'angolo β  è uguale all'angolo  φ

 

dopo un tempo dt, r spazzola un angolo φ	dopo un tempo dt, u spazzola un angolo β = φ
r fa un giro completo in un tempo T	u fa un giro completo in un tempo T
v è perpendicolare a r	a è perpendicolare a u  → a  ┴ v
	ma  u=v    v=rω
L'accelerazione in un punto è parallelo al raggio in quel punto ed è diretto verso il centro ( a  ┴ v,  v ┴ r → a ||  r)

 

Con un po' di matematica troviamo lo stesso risultato in maniera più meccanica (in quanto i calcoli li può fare anche un PC)

 

Divide et impera. Era la strategia degli eserciti romani: dividi gli avversari e vinci

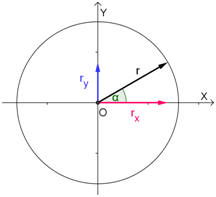
Scomponiamo il vettore r nelle componenti lungo gli assi X e Y

 

Ricorda