LABORATORIO DI FISICA
piano inclinatoattendere caricamento applet
|
||
| Luciano Troilo, Creato con GeoGebra |
MISURE
ATTIVITA':
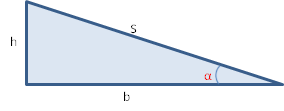
Verifica sperimentale della legge di Galilei:
"Se un corpo si muove senza attrito lungo un piano inclinato, lo spazio percorso è sempre proporzionale al quadrato del tempo impiegato a percorrerlo."
-
Premi "START" per far partire la simulazione
-
Prendi i tempi ad ogni traguardo cliccando sul pulsante "TIMER". Riporta i dati in un foglio di calcolo.
-
Fai attenzione al separatore dei decimali: qui è usato il "punto". Controlla se il tuo foglio di lavoro (com'è probabile) faccia invece uso della virgola.
-
Ripeti la misura almeno tre volte, senza cambiare l'altezza h. Fai la media delle misure.
Elaborazione dati sperimentali con Excel
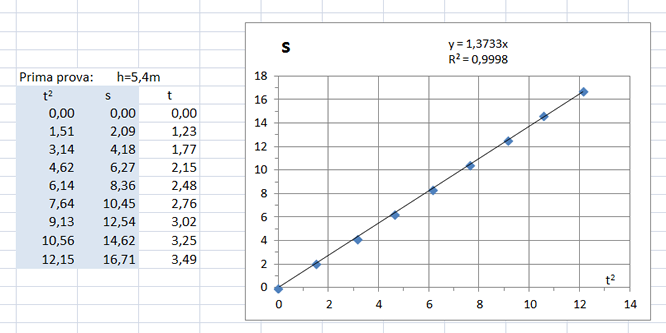
Per verificare se s è proporzionale al quadrato del tempo:
-
Aggiungi una colonna t^2 ai tuoi dati
-
Rappresenta in un piano cartesiano i punti (t^2, S). Con Excel:
-
selezionare la colonna t^2 e la colonna s
-
inserire grafico a dispersione,
-
-
Disegna la retta che meglio approssima i punti. Con Excel:
-
cliccare con il tasto destro del mouse su uno dei punti rappresentati,
-
dal menu contestuale selezionare "aggiungi linea di tendenza",
-
spuntare le ultime tre caselle:
-
imposta intercetta = 0,0
-
visualizza l'equazione sul grafico
-
visualizza il valore di R quadradrato (coefficiente di determinazione)
-
-
R quadrato (detto anche coefficiente di determinazione) rappresenta un indicatore che, partendo dalla retta di regressione, sintetizza in un unico valore di quanto la grandezza analizzata si discosta mediamente da tale retta.
Può assumere valori compresi fra 0 e 1.
Se è pari a 1 allora esiste una perfetta relazione lineare fra il fenomeno analizzato e la sua retta di regressione.
Se pari a 0 non esiste alcuna relazione lineare fra le due variabili mentre i valori compresi fra 0 e 1 forniscono una indicazione sulla efficacia della retta di regressione di sintetizzare l’oggetto dell’analisi.
-
-
Ripeti la simulazione dell'esperimento per diverse altezze h. Facendo variare l'altezza h ottieni sempre lo stesso tipo di curva che meglio approssima i valori sperimentali?
-
Cosa varia nell'equazione della curva cambiando il valore di h?
Puoi affermare che i nostri dati sperimentali confermano l'ipotesi di Galilei? Giustifica la tua risposta.
Scarica il foglio di lavoro Excel
TEORIA
Gli esperimenti di Galilei
“In un regolo, o vogliàn dir corrente, di legno, lungo circa 12 braccia, e largo per un verso mezzo braccio e per l’altro 3 dita, si era in questa minor larghezza incavato un canaletto, poco più largo d’un dito; tiratolo drittissimo, e, per averlo ben pulito e liscio, incollatovi dentro una carta pecora zannata e lustrata al possibile, si faceva in esso scendere una palla di bronzo durissimo, ben rotondata e pulita”.
Con questi accorgimenti Galileo vuole rendere trascurabili gli effetti dell’attrito.
“Elevando sopra il piano orizzontale una delle estremità (del regolo) un braccio o due ad arbitrio, si lasciava (…) scendere per il detto canale la palla, notando (…) il tempo che consumava nello scorrerlo tutto, replicando il medesimo atto molte volte per assicurarsi bene della quantità del tempo (…). Fatta e stabilita precisamente tale operazione, facemmo scender la medesima palla solamente per la quarta parte della lunghezza di esso canale; e misurato il tempo della sua scesa, si trovava sempre puntualissimamente esser la metà dell’altro”.
Ripetendo la misura per distanze diverse, Galileo deduce che lo spazio percorso è sempre proporzionale al quadrato del tempo impiegato a percorrerlo. In altri termini, se i tempi sono rappresentati da 1, 2, 3, 4, 5… gli spazi percorsi sono rispettivamente rappresentati da 1, 4, 9, 16, 25… Questa è la prima descrizione del tipo di moto definito, da Galileo in poi, “uniformemente accelerato”.

Piano inclinato di Galilei
sitografia: http://catalogo.museogalileo.it/
APPROFONDIMENTI

ESERCIZI
Calcolare l'accelerazione lungo il piano inclinato |
Calcolare il valore più probabile dell'accelerazione lungo il piano inclinato considerando i dati sperimentali presi nelle condizioni del problema di sinistra |
|||||||||||||||||||||
b=18mh=5m
|
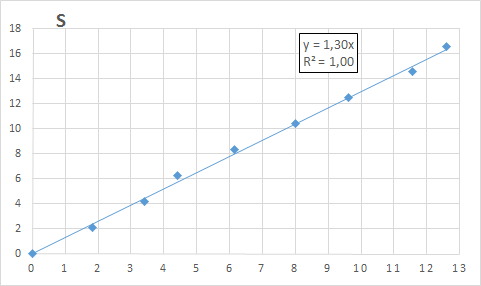
Scelti base e altezza pari rispettivamente a 18m e 5m,Riportiamo t2 ed s in foglio di Excel e ricaviamo la retta che meglio approssima i dati.
|
|||||||||||||||||||||
|
Quindi l'equazione del moto è:s=1,30t2Ma il coefficiente di t2 è pari alla metà dell'accelerazione che quindi risulterà:gs = 1,30m/s2 * 2 =2,60m/s2(abbiamo fatto i calcoli con 2 cifre significative) |